前向传播以及BP（反向传播）.

发表于   |   更新于 | 分类于 | 阅读次数
字数统计: 3k | 阅读时长 ≈ 14
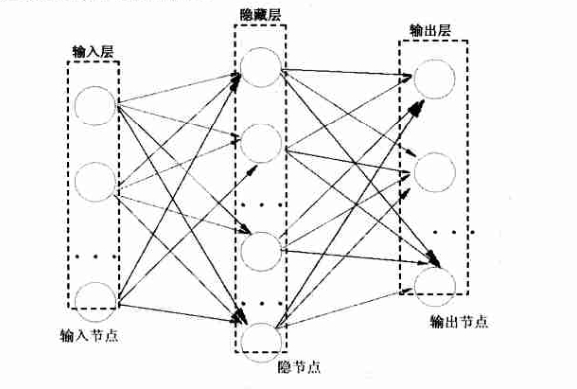
  1. BP（backward propogation）神经网络 简单理解，神经网络就是一种高端的拟合技术。教程也非常多，但实际上个人觉得看看斯坦福的相关学习资料就足够，并且国内都有比较好的翻译：

  2. 神经网络的过程

    1. 简单说，就是我有一堆已知的输入向量（每个向量可能有多维），每次读取一个向量（可能会有多维度），每个特征维度成为上图的输入层中一个输入节点。
    2. 每个维度的数值，将自己的一部分按照权值分配送给隐藏层。写程序时第一次的权值怎么办呢？其实（-1，1）随机化（绝不是0~1随机化）就好了，后续会逐渐修正。
    3. 这样隐含层每个节点同样有了自己的数值，同样道理，乘以权值再经过激活函数（根据需求选择，分类问题一般是 sigmoid 函数，数值拟合一般是 purelin 函数，也有特殊函数），最后传给输出节点。每个输出节点的每个值对应输出向量的一个特征维度

    至此，我们完成了一次 forward pass 过程，方向是：输入层⇒⇒输出层。

    1. 熟悉神经网络的同学肯定知道，神经网络使用时有“训练”、“测试”两部分。我们现在考虑训练过程。每次 forward pass 过程之后，输出层的值与真实值之间，存在一个差，这个差记为 δδ。 此时我们根据公式，将误差作为参数传给隐藏层节点。
    2. 这些误差有什么用呢？还记得我们各个层之间的随机化的权值么？就是用来修正这个权值的。同理，修改输入层与隐藏层之间的权值，我们的视角到达输入层。

    至此，我们完成了一次 backward pass 过程，方向是：输入层⇐⇐输出层。 第一个样本的一套做完了，即 forward pass + backward pass。 接下来呢？再做第二个样本的一套，并把误差与上一个样本误差相加；第三个样本的一套，加误差；……第N个样本的一套，加误差。等到所有样本都过了一遍，看误差和是否小于阈值（根据实际情况自由设定）时。如果不小于则进行下一整套样本，即：

    • 清零误差；第一个样本，加误差；第二个样本，加误差；……第N个样本，加误差。误差和是否小于阈值……
    • 误差和达到阈值，妥了，不训练了此时输入一个测试样本，将各个特征维度的数值输入到输入层节点，一次 forward pass，得到的输出值就是我们的预测值。

  3. 易错点 既然这么通俗易懂，为什么实现中会出现错误呢？下面说说几个遇到的错误：

    1. 输入节点，究竟是每个样本的特征维度一个节点？还是每个样本一个节点？以为每个样本对应一个输出节点，是错误的。答案是每个特征一个输入节点；
    2. bias 必不可少！bias 是一个数值偏移量，不受上一层神经元的影响，在每个神经元汇总上一层的信息之后，都需要进行偏移之后再作为激活函数的输入。开头教程中有说明，这是为什么呢？举个例子，如果我们学习 XOR 问题，2个输入节点是0、0，如果没有 bias 所有隐含层节点都是同一个值，产生对称失效问题；
    3. 神经网络有多少隐含层、每个隐含层多少神经元、学习效率，都是需要调试的。没有确解，但要保证每次循环中，样本的误差和呈下降趋势

    最后，是我参考的C++实现代码：

·BP神经网络头文件

pragma once

include

include

include

include

include

using namespace std;

define innode 2 //输入结点数

define hidenode 4 //隐含结点数

define hidelayer 1 //隐含层数

define outnode 1 //输出结点数

define learningRate 0.9//学习速率，alpha

// --- -1~1 随机数产生器 —-
inline double get_11Random() // -1 ~ 1
{
return ((2.0(double)rand()/RAND_MAX) - 1);
}
// --- sigmoid 函数 —-
inline double sigmoid(double x)
{
double ans = 1 / (1+exp(-x));
return ans;
}
// --- 输入层节点。包含以下分量：—-
// 1.value: 固定输入值；
// 2.weight: 面对第一层隐含层每个节点都有权值；
// 3.wDeltaSum: 面对第一层隐含层每个节点权值的delta值累积
typedef struct inputNode
{
double value;
vector weight, wDeltaSum;
}inputNode;
// --- 输出层节点。包含以下数值：—-
// 1.value: 节点当前值；
// 2.delta: 与正确输出值之间的delta值；
// 3.rightout: 正确输出值
// 4.bias: 偏移量
// 5.bDeltaSum: bias的delta值的累积，每个节点一个
typedef struct outputNode // 输出层节点
{
double value, delta, rightout, bias, bDeltaSum;
}outputNode;
// --- 隐含层节点。包含以下数值：—-
// 1.value: 节点当前值；
// 2.delta: BP推导出的delta值；
// 3.bias: 偏移量
// 4.bDeltaSum: bias的delta值的累积，每个节点一个
// 5.weight: 面对下一层（隐含层/输出层）每个节点都有权值；
// 6.wDeltaSum： weight的delta值的累积，面对下一层（隐含层/输出层）每个节点各自积累
typedef struct hiddenNode // 隐含层节点
{
double value, delta, bias, bDeltaSum;
vector weight, wDeltaSum;
}hiddenNode;
// --- 单个样本 —-
typedef struct sample
{
vector in, out;
}sample;
// --- BP神经网络 —-
class BpNet
{
public:
BpNet(); //构造函数
void forwardPropagationEpoc(); // 单个样本前向传播
void backPropagationEpoc(); // 单个样本后向传播
void training (static vector sampleGroup, double threshold);// 更新 weight, bias
void predict (vector& testGroup); // 神经网络预测
void setInput (static vector sampleIn); // 设置学习样本输入
void setOutput(static vector sampleOut); // 设置学习样本输出
public:
double error;
inputNode inputLayer[innode]; // 输入层（仅一层）
outputNode outputLayer[outnode]; // 输出层（仅一层）
hiddenNode hiddenLayer[hidelayer][hidenode]; // 隐含层（可能有多层）
};

·BP神经网络源文件

include “BPnet.h”

using namespace std;
BpNet::BpNet()
{
srand((unsigned)time(NULL)); // 随机数种子
error = 100.f; // error初始值，极大值即可
// 初始化输入层
for (int i = 0; i < innode; i++)
{
inputLayer[i] = new inputNode();
for (int j = 0; j < hidenode; j++)
{
inputLayer[i]->weight.push_back(get_11Random());
inputLayer[i]->wDeltaSum.push_back(0.f);
}
}
// 初始化隐藏层
for (int i = 0; i < hidelayer; i++)
{
if (i == hidelayer - 1)
{
for (int j = 0; j < hidenode; j++)
{
hiddenLayer[i][j] = new hiddenNode();
hiddenLayer[i][j]->bias = get_11Random();
for (int k = 0; k < outnode; k++)
{
hiddenLayer[i][j]->weight.push_back(get_11Random());
hiddenLayer[i][j]->wDeltaSum.push_back(0.f);
}
}
}
else
{
for (int j = 0; j < hidenode; j++)
{
hiddenLayer[i][j] = new hiddenNode();
hiddenLayer[i][j]->bias = get_11Random();
for (int k = 0; k < hidenode; k++) {hiddenLayer[i][j]->weight.push_back(get_11Random());}
}
}
}
// 初始化输出层
for (int i = 0; i < outnode; i++)
{
outputLayer[i] = new outputNode();
outputLayer[i]->bias = get_11Random();
}
}
void BpNet::forwardPropagationEpoc()
{
// forward propagation on hidden layer
for (int i = 0; i < hidelayer; i++)
{
if (i == 0)
{
for (int j = 0; j < hidenode; j++)
{
double sum = 0.f;
for (int k = 0; k < innode; k++)
{
sum += inputLayer[k]->value inputLayer[k]->weight[j];
}
sum += hiddenLayer[i][j]->bias;
hiddenLayer[i][j]->value = sigmoid(sum);
}
}
else
{
for (int j = 0; j < hidenode; j++)
{
double sum = 0.f;
for (int k = 0; k < hidenode; k++)
{
sum += hiddenLayer[i-1][k]->value hiddenLayer[i-1][k]->weight[j];
}
sum += hiddenLayer[i][j]->bias;
hiddenLayer[i][j]->value = sigmoid(sum);
}
}
}
// forward propagation on output layer
for (int i = 0; i < outnode; i++)
{
double sum = 0.f;
for (int j = 0; j < hidenode; j++)
{
sum += hiddenLayer[hidelayer-1][j]->value hiddenLayer[hidelayer-1][j]->weight[i];
}
sum += outputLayer[i]->bias;
outputLayer[i]->value = sigmoid(sum);
}
}
void BpNet::backPropagationEpoc()
{
// backward propagation on output layer
// -- compute delta
for (int i = 0; i < outnode; i++)
{
double tmpe = fabs(outputLayer[i]->value-outputLayer[i]->rightout);
error += tmpe tmpe / 2;
outputLayer[i]->delta
= (outputLayer[i]->value-outputLayer[i]->rightout)(1-outputLayer[i]->value)outputLayer[i]->value;
}
// backward propagation on hidden layer
// -- compute delta
for (int i = hidelayer - 1; i >= 0; i—) // 反向计算
{
if (i == hidelayer - 1)
{
for (int j = 0; j < hidenode; j++)
{
double sum = 0.f;
for (int k=0; kdelta hiddenLayer[i][j]->weight[k];}
hiddenLayer[i][j]->delta = sum (1 - hiddenLayer[i][j]->value) hiddenLayer[i][j]->value;
}
}
else
{
for (int j = 0; j < hidenode; j++)
{
double sum = 0.f;
for (int k=0; kdelta hiddenLayer[i][j]->weight[k];}
hiddenLayer[i][j]->delta = sum (1 - hiddenLayer[i][j]->value) hiddenLayer[i][j]->value;
}
}
}
// backward propagation on input layer
// -- update weight delta sum
for (int i = 0; i < innode; i++)
{
for (int j = 0; j < hidenode; j++)
{
inputLayer[i]->wDeltaSum[j] += inputLayer[i]->value hiddenLayer[0][j]->delta;
}
}
// backward propagation on hidden layer
// -- update weight delta sum & bias delta sum
for (int i = 0; i < hidelayer; i++)
{
if (i == hidelayer - 1)
{
for (int j = 0; j < hidenode; j++)
{
hiddenLayer[i][j]->bDeltaSum += hiddenLayer[i][j]->delta;
for (int k = 0; k < outnode; k++)
{ hiddenLayer[i][j]->wDeltaSum[k] += hiddenLayer[i][j]->value outputLayer[k]->delta; }
}
}
else
{
for (int j = 0; j < hidenode; j++)
{
hiddenLayer[i][j]->bDeltaSum += hiddenLayer[i][j]->delta;
for (int k = 0; k < hidenode; k++)
{ hiddenLayer[i][j]->wDeltaSum[k] += hiddenLayer[i][j]->value hiddenLayer[i+1][k]->delta; }
}
}
}
// backward propagation on output layer
// -- update bias delta sum
for (int i = 0; i < outnode; i++) outputLayer[i]->bDeltaSum += outputLayer[i]->delta;
}
void BpNet::training(static vector sampleGroup, double threshold)
{
int sampleNum = sampleGroup.size();
while(error > threshold)
//for (int curTrainingTime = 0; curTrainingTime < trainingTime; curTrainingTime++)
{
cout << “training error: “ << error << endl;
error = 0.f;
// initialize delta sum
for (int i = 0; i < innode; i++) inputLayer[i]->wDeltaSum.assign(inputLayer[i]->wDeltaSum.size(), 0.f);
for (int i = 0; i < hidelayer; i++){
for (int j = 0; j < hidenode; j++)
{
hiddenLayer[i][j]->wDeltaSum.assign(hiddenLayer[i][j]->wDeltaSum.size(), 0.f);
hiddenLayer[i][j]->bDeltaSum = 0.f;
}
}
for (int i = 0; i < outnode; i++) outputLayer[i]->bDeltaSum = 0.f;
for (int iter = 0; iter < sampleNum; iter++)
{
setInput(sampleGroup[iter].in);
setOutput(sampleGroup[iter].out);
forwardPropagationEpoc();
backPropagationEpoc();
}
// backward propagation on input layer
// -- update weight
for (int i = 0; i < innode; i++)
{
for (int j = 0; j < hidenode; j++)
{
inputLayer[i]->weight[j] -= learningRate inputLayer[i]->wDeltaSum[j] / sampleNum;
}
}
// backward propagation on hidden layer
// -- update weight & bias
for (int i = 0; i < hidelayer; i++)
{
if (i == hidelayer - 1)
{
for (int j = 0; j < hidenode; j++)
{
// bias
hiddenLayer[i][j]->bias -= learningRate hiddenLayer[i][j]->bDeltaSum / sampleNum;
// weight
for (int k = 0; k < outnode; k++)
{ hiddenLayer[i][j]->weight[k] -= learningRate hiddenLayer[i][j]->wDeltaSum[k] / sampleNum; }
}
}
else
{
for (int j = 0; j < hidenode; j++)
{
// bias
hiddenLayer[i][j]->bias -= learningRate hiddenLayer[i][j]->bDeltaSum / sampleNum;
// weight
for (int k = 0; k < hidenode; k++)
{ hiddenLayer[i][j]->weight[k] -= learningRate hiddenLayer[i][j]->wDeltaSum[k] / sampleNum; }
}
}
}
// backward propagation on output layer
// -- update bias
for (int i = 0; i < outnode; i++)
{ outputLayer[i]->bias -= learningRate outputLayer[i]->bDeltaSum / sampleNum; }
}
}
void BpNet::predict(vector& testGroup)
{
int testNum = testGroup.size();
for (int iter = 0; iter < testNum; iter++)
{
testGroup[iter].out.clear();
setInput(testGroup[iter].in);
// forward propagation on hidden layer
for (int i = 0; i < hidelayer; i++)
{
if (i == 0)
{
for (int j = 0; j < hidenode; j++)
{
double sum = 0.f;
for (int k = 0; k < innode; k++)
{
sum += inputLayer[k]->value inputLayer[k]->weight[j];
}
sum += hiddenLayer[i][j]->bias;
hiddenLayer[i][j]->value = sigmoid(sum);
}
}
else
{
for (int j = 0; j < hidenode; j++)
{
double sum = 0.f;
for (int k = 0; k < hidenode; k++)
{
sum += hiddenLayer[i-1][k]->value hiddenLayer[i-1][k]->weight[j];
}
sum += hiddenLayer[i][j]->bias;
hiddenLayer[i][j]->value = sigmoid(sum);
}
}
}
// forward propagation on output layer
for (int i = 0; i < outnode; i++)
{
double sum = 0.f;
for (int j = 0; j < hidenode; j++)
{
sum += hiddenLayer[hidelayer-1][j]->value hiddenLayer[hidelayer-1][j]->weight[i];
}
sum += outputLayer[i]->bias;
outputLayer[i]->value = sigmoid(sum);
testGroup[iter].out.push_back(outputLayer[i]->value);
}
}
}
void BpNet::setInput(static vector sampleIn)
{
for (int i = 0; i < innode; i++) inputLayer[i]->value = sampleIn[i];
}
void BpNet::setOutput(static vector sampleOut)
{
for (int i = 0; i < outnode; i++) outputLayer[i]->rightout = sampleOut[i];
}

·BP神经网络main函数实现：（我们这里使用典型非线性问题：XOR 测试）：

include “BPnet.h”

int main()
{
BpNet testNet;
// 学习样本
vector samplein[4];
vector sampleout[4];
samplein[0].push_back(0); samplein[0].push_back(0); sampleout[0].push_back(0);
samplein[1].push_back(0); samplein[1].push_back(1); sampleout[1].push_back(1);
samplein[2].push_back(1); samplein[2].push_back(0); sampleout[2].push_back(1);
samplein[3].push_back(1); samplein[3].push_back(1); sampleout[3].push_back(0);
sample sampleInOut[4];
for (int i = 0; i < 4; i++)
{
sampleInOut[i].in = samplein[i];
sampleInOut[i].out = sampleout[i];
}
vector sampleGroup(sampleInOut, sampleInOut + 4);
testNet.training(sampleGroup, 0.0001);
// 测试数据
vector testin[4];
vector testout[4];
testin[0].push_back(0.1); testin[0].push_back(0.2);
testin[1].push_back(0.15); testin[1].push_back(0.9);
testin[2].push_back(1.1); testin[2].push_back(0.01);
testin[3].push_back(0.88); testin[3].push_back(1.03);
sample testInOut[4];
for (int i = 0; i < 4; i++) testInOut[i].in = testin[i];
vector testGroup(testInOut, testInOut + 4);
// 预测测试数据，并输出结果
testNet.predict(testGroup);
for (int i = 0; i < testGroup.size(); i++)
{
for (int j = 0; j < testGroup[i].in.size(); j++) cout << testGroup[i].in[j] << “\\t”;
cout << “— prediction :”;
for (int j = 0; j < testGroup[i].out.size(); j++) cout << testGroup[i].out[j] << “\\t”;
cout << endl;
}
system(“pause”);
return 0;
}

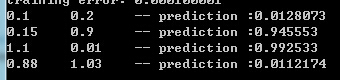
-- 最终的实验结果基本正确： 这里写图片描述

(っ•̀ω•́)っ✎⁾⁾ 坚持技术学习、内容输出与分享，您的支持将鼓励我继续创作！(*/ω＼*)
( • ̀ω•́ )✧如有疑问或需要技术讨论，请留言或发邮件到 aclearzhang@qq.com.(*･ω< ) 
  • 本文作者：： AClearZhang
  • 本文链接：： 1246.html
  • 版权声明： 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 3.0 许可协议。转载请注明出处！